Paper Explain: "Grams: Gradient Descent with Adaptive Momentum Scaling"

See the original paper on arXiv.

Introduction

#

Gradient Descent with Adaptive Momentum Scaling (Grams) is a novel optimization algorithm that decouples the direction and magnitude of parameter updates in deep learning. Unlike traditional optimizers that directly integrate momentum into updates, Grams separates the update direction, derived from current gradients, from momentum, which is used solely for adaptive magnitude scaling. This approach enables Grams to achieve improved loss descent compared to state-of-the-art cautious and momentum-based optimizers.

The Grams algorithm is expressed as:

$$ \begin{align*} m_{t} &:= \beta_{1} m_{t-1} + (1 - \beta_{1}) g_{t} \\ v_{t} &:= \beta_{2} v_{t-1} + (1 - \beta_{2}) g_{t}^{2} \\ \hat{m}_{t} &:= \frac{m_{t}}{1 - \beta_{1}^{t}} \\ \hat{v}_{t} &:= \frac{v_{t}}{1 - \beta_{2}^{t}} \\ u_{t} &:= \frac{\hat{m}_{t}}{\sqrt{\hat{v}_{t}} + \epsilon} \\ \hat{u}_{t} &:= \mathrm{sign}(g_{t}) \circ |u_{t}| \\ w_{t} &:= w_{t-1} - \eta_{t} \hat{u}_{t}, \end{align*} $$

where \(w_t\) is the weight at time step \(t\), \( g_t := \nabla_{w} \mathcal{L}(w_{t-1}) \) is the current gradient, \(\beta_1\) and \(\beta_2\) are decay rates for the moment estimates, \(\eta_t\) is the learning rate, and \(\epsilon\) is a small constant for numerical stability, \( \eta_t \) is the learning rate at step \(t\), \( | \cdot | \) is element-wise absolute value, \( \circ \) denotes Hadamard product, and \( \mathrm{sign}(\cdot) \) is the element-wise sign function.

Compare to the Adam optimizer, instead of update \(w_t\) with \(w_t := w_{t-1} - \eta u_t\), Grams realigns the update direction \(u_t\) to the gradient direction \(g_t\), which is called adaptive momentum scaling.

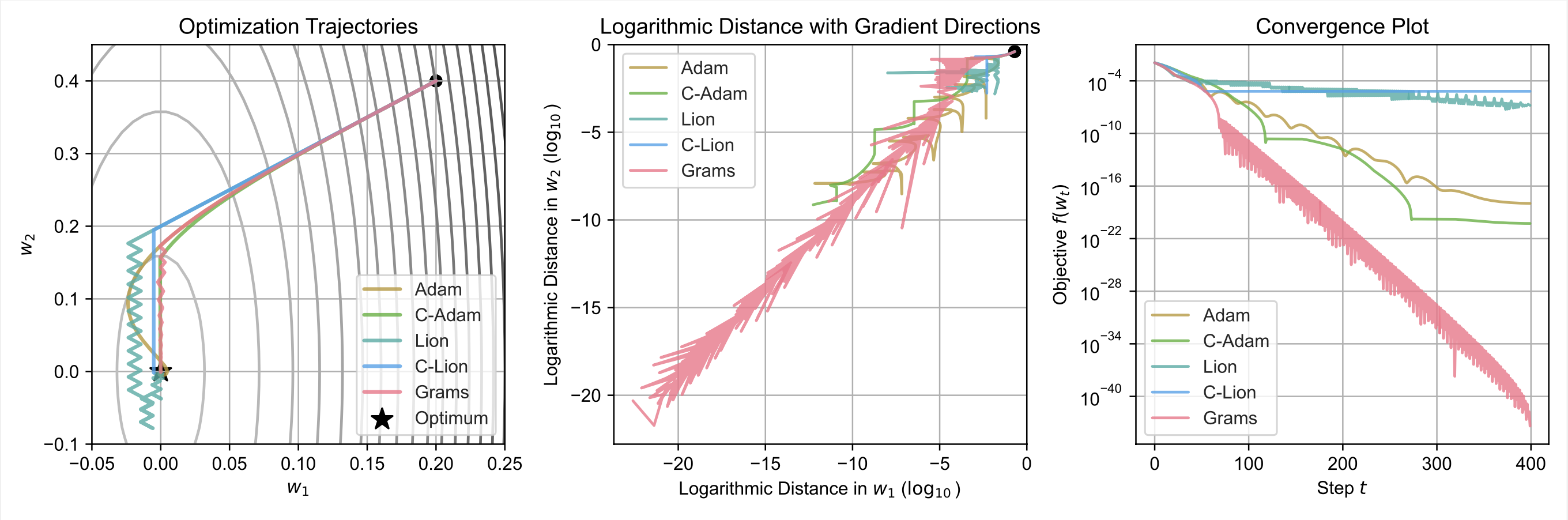
In the figures above, we analyze the optimization trajectories and convergence behavior of several algorithms—Adam¹, Lion², their cautious variants (C-Adam, C-Lion) ³, and the proposed Grams optimizer—on a simple convex objective function.

The first figure illustrates the optimization trajectories in the parameter space \((w_1, w_2)\). It is evident that Grams combines beneficial features from both cautious Adam and Lion optimizers. Compared to standard Adam, Grams takes a direct “shortcut” as \(w_1\) approaches the optimal value, significantly reducing oscillations around the optimum. Unlike cautious Adam, Grams adopts a zig-zag update pattern similar to Lion in the final stages of optimization, but notably achieves faster and more precise convergence.

The second figure provides a logarithmic visualization of parameter convergence toward the optimum. Here, the advantages of Grams are further clarified: it maintains a more direct and tightly controlled trajectory toward the optimal solution, surpassing Adam and its cautious variant in both stability and speed.

The third figure illustrates the convergence of the objective function value over optimization steps. While C-Adam displays a smooth, monotonically decreasing trend, Grams exhibits significantly larger decreases per step, highlighting its superior efficiency in rapidly approaching the optimum. This larger magnitude of decrease allows Grams to reach dramatically lower objective function values quicker and with fewer oscillations than Adam, Lion, and their cautious variants, underscoring Grams’ enhanced optimization performance. This observation also aligns with our theoretical analysis in the theory section.

Theoretical Analysis

#

We provide a theoretical analysis of the Grams optimizer, focusing on the convergence properties and optimization dynamics. Our analysis reveals that Grams exhibits superior convergence behavior compared to Adam and C-Adam. For proofs and more details, please refer to the paper.

Notation

#

For two vectors \(u, v\in \R^d\), we use \(\langle u, v\rangle\) to denote the standard inner product in the Euclidean space. Given a vector \(x \in \mathbb{R}^d\), we use \(\mathbf{1}_{x \geq 0} \in \mathbb{R}^d\) to denote the vector where each entry indicates whether the corresponding entry of \(x\) is non-negative, i.e., for each \(i \in [d]\), \((\mathbf{1}_{x \geq 0})_i = 0\) if \(x_i \geq 0\), and \((\mathbf{1}_{x \geq 0})_i = 1\) otherwise.

Loss Descent Analysis

#

First, we provide a detailed analysis of the loss descent properties of the Cautious Adam optimizer.

Lemma 1 (Lemma 3.9 in the paper). Suppose that \( \mathcal{L} : \mathbb{R}^d \to \mathbb{R} \) is \(L\)-smooth. Let \( \Delta \mathcal{L}_{w_{t+1}^{\mathrm{C}},w_{t}} := \mathcal{L}(w_{t+1}^{\mathrm{C}}) - \mathcal{L}(w_{t}) \), and \( w_{t+1}^{\mathrm{C}} \) is updated from \( w_{t} \) by the Cautious Adam optimizer. Then, we have the following:

• Part 1: It holds that

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{C}}, w_t} \leq -\eta_t \langle u_t \circ g_t, {\bf 1}_{u_t \circ g_t \geq 0}\rangle + \frac{L \eta_t^2}{2}\| u_t\|_2^2, $$

• Part 2: It holds that

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{C}}, w_t} \geq -\eta_t \langle u_t \circ g_t, {\bf 1}_{u_t \circ g_t \geq 0}\rangle. $$

• Part 3: If \(\eta_t \leq \frac{2}{L\|u_t\|^2_2} \langle u_t \circ g_t, {\bf 1}_{u_t \circ g_t \geq 0}\rangle\), then we have

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{C}}, w_t} \leq 0. $$

Then, we provide a detailed analysis of the loss descent properties of the Grams optimizer.

Lemma 2 (Lemma 4.1 in the paper). Suppose that \( \mathcal{L} : \mathbb{R}^d \to \mathbb{R} \) is \(L\)-smooth. Let \( \Delta \mathcal{L}_{w_{t+1}^{\mathrm{Grams}},w_{t}} := \mathcal{L}(w_{t+1}^{\mathrm{Grams}}) - \mathcal{L}(w_{t}) \), and \( w_{t+1}^{\mathrm{Grams}} \) is updated from \( w_{t} \) by the Grams optimizer. Then, we have the following:

• Part 1: It holds that

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{Grams}}, w_{t}} \leq - \eta_{t} \langle |g_t|, |u_t| \rangle + \frac{L \eta_t^2}{2} \| u_t \|_2^2. $$

• Part 2: It holds that

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{Grams}}, w_{t}} \geq - \eta_t \langle |g_t|, |u_t| \rangle. $$

• Part 3: If \( \eta_t \leq \frac{2}{L\|u_t\|^2} \langle |g_t|, |u_t| \rangle \), then we have

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{Grams}}, w_{t}} \leq 0. $$

Based on the above lemmas, we see that Grams achieves better loss descent properties compared to Cautious Adam. We formalized this analysis in the following theorem.

Theorem 1 (Theorem 4.3 in the paper). Suppose that \( \mathcal{L} : \mathbb{R}^d \to \mathbb{R} \) is \(L\)-smooth. For any parameter vector \( w \) at optimization step \( t \), let \( w^{\mathrm{Grams}} \) and \( w^{\mathrm{C}} \) be the update of Cautious Adam and Grams, respectively. If the stepsize \( \eta_t \) satisfies

$$ \eta_t \leq \frac{2}{L\|u_t\|^2} \cdot \min\{\langle u_t \circ g_t, {\bf 1}_{u_t \circ g_t \geq 0} \rangle, \langle u_t \circ g_t, {\bf 1}_{u_t \circ g_t < 0}\rangle\}, $$

then we have

$$ \Delta \mathcal{L}_{w_{t+1}^{\mathrm{Grams}}, w_t} \leq \Delta \mathcal{L}_{w_{t+1}^{\mathrm{C}}, w_t} \leq 0. $$

This theorem shows that Grams achieves better loss descent properties compared to Cautious Adam under the relax assumption, providing theoretical support for the superior optimization performance of Grams.

Hamiltonian Dynamics Analysis

#

We further analyze the optimization dynamics of the Grams optimizer from the perspective of Hamiltonian dynamics. We show that the Grams optimizer can be interpreted as a Hamiltonian system with a modified Hamiltonian function, which provides insights into the optimization behavior of Grams.

The Hamiltonian dynamics of the Grams optimizer is expressed as:

$$ \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} w_t := & ~ -\mathrm{sign}(\nabla \mathcal{L}(w_t)) \circ |\nabla \mathcal{K}(s_t)| - \Phi_t(\nabla \mathcal{L}(w_t)) \\ \frac{\mathrm{d}}{\mathrm{d}t} s_t := & ~ \nabla \mathcal{L}(w_t) - \Psi_t(\nabla \mathcal{K}(s_t)), \end{align*} $$

where \(w_t\) and \(s_t\) represent the parameters and momentum, respectively; \(\nabla \mathcal{L}(w_t)\) and \(\nabla \mathcal{K}(s_t)\) denote gradients of the loss and kinetic functions, and \(\Phi\) and \(\Psi\) are two monotonic mappings satisfying \( \langle x, \Phi(x) \rangle \geq 0 \) and \( \langle x, \Psi(x) \rangle \geq 0 \).

Then, we take the derivative of the Hamiltonian function \(H(w_t, s_t) = \mathcal{L}(w_t) + \mathcal{K}(s_t)\) with respect to time \(t\) to obtain the following:

$$ \begin{align*} \Delta^{\mathrm{Grams}}_{H}(w_t,s_t) := & ~ \frac{\mathrm{d}}{\mathrm{d}t} H(w_t, s_t) \\ = & ~ \langle \nabla \mathcal{L}(w_t), \nabla \mathcal{K}(s_t) \rangle - \langle |\nabla \mathcal{L}(w_t)|, |\nabla \mathcal{K}(s_t)| \rangle - \Delta_H(w_t,s_t) \\ \leq & ~ 0. \end{align*} $$

Similarly, we can derive the objective function under the Hamiltonian dynamics:

$$ \begin{align*} \Delta^{\mathrm{Grams}}_{\mathcal{L}}(w_t) := & ~ \frac{\mathrm{d}}{\mathrm{d}t} \mathcal{L}(w_t) \\ = & ~ \langle \nabla \mathcal{L}(w_t), \nabla \mathcal{K}(s_t) \rangle - \langle |\nabla \mathcal{L}(w_t)|, |\nabla \mathcal{K}(s_t)| \rangle - \Delta_{\mathcal{L}}(w_t, s_t). \end{align*} $$

In these two equations, \( \Delta_H(w_t, s_t) \) and \( \Delta_{\mathcal{L}}(w_t, s_t) \) are the changes in the Hamiltonian and loss functions, respectively.

Similarly, we can have the derivative of the Hamiltonian function and the objective function for the Cautious Adam optimizer, then we have:

$$ \begin{align*} \Delta^{\mathrm{C}}_{H}(w_t,s_t) = & ~ \langle x_t, \mathbf{1} - \mathbf{1}_{x_t \geq 0} \rangle - \Delta_H(w_t,s_t) \\ \Delta^{\mathrm{C}}_{\mathcal{L}}(w_t) = & ~ \langle x_t, \mathbf{1} - \mathbf{1}_{x_t \geq 0} \rangle - \Delta_{\mathcal{L}}(w_t, s_t), \end{align*} $$

Comparing \(\Delta^{\mathrm{Grams}}{H}(w_t,s_t)\) with \(\Delta^{\mathrm{C}}{H}(w_t,s_t)\), we observe that the Hamiltonian update in the Grams optimizer is always strictly negative, whereas this condition does not necessarily hold for the Cautious Adam optimizer.

Moreover, for the objective function, we have the following theorem:

Theorem 2 (Convergence Comparison of Hamiltonian Dynamics between Grams and Cautious Optimizers, Theorem 4.7 in the paper). Following the Hamiltonian dynamics of the Grams and Cautious Adam optimizers, we have:

$$ \Delta^{\mathrm{Grams}}_{\mathcal{L}}(w_t) \leq \Delta^{\mathrm{C}}_{\mathcal{L}}(w_t). $$

This theorem demonstrates that the Grams optimizer achieves same or better convergence properties compared to the Cautious Adam optimizer under the Hamiltonian dynamics, providing further theoretical support for the superior optimization performance of Grams.

Experimental Results

#

We conduct extensive experiments to evaluate the performance of the Grams optimizer on various datasets and deep learning models. Our experiments demonstrate that Grams consistently outperforms state-of-the-art cautious and momentum-based optimizers in terms of optimization efficiency and convergence speed. The results are summarized in the following tables:

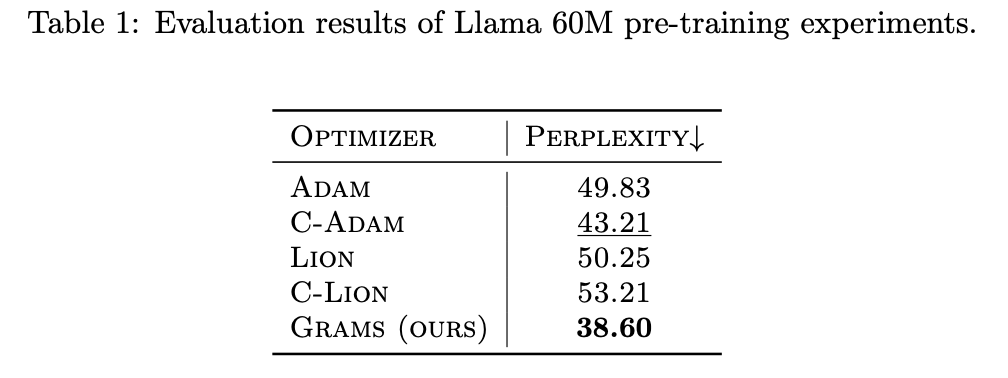
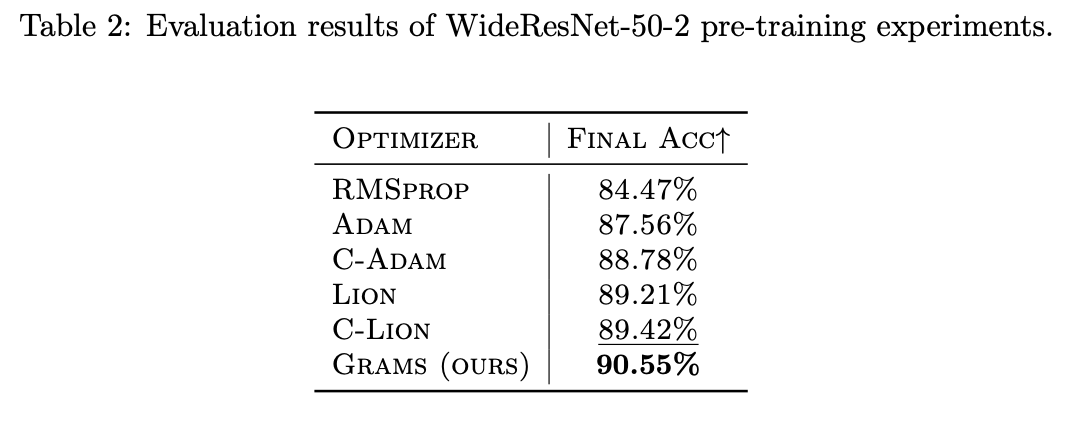
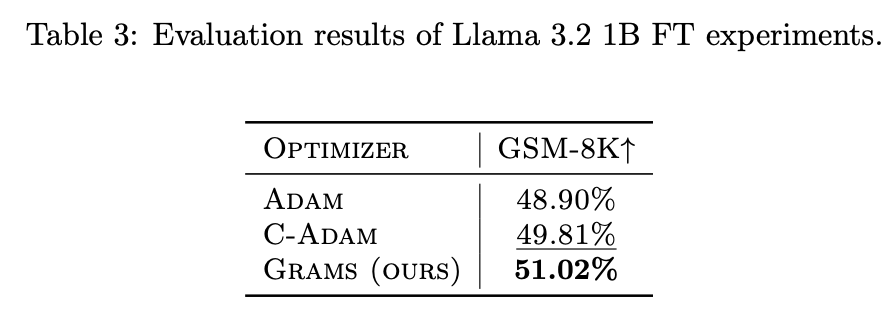
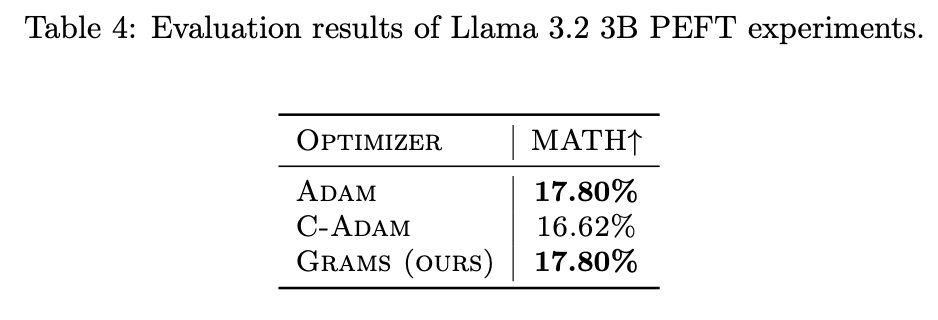
The experimental results show that Grams achieves state-of-the-art performance across different datasets and models, highlighting its effectiveness in optimizing deep learning models.

Conclusion

#

This paper introduces the Grams optimizer, a novel optimization algorithm that decouples the direction and magnitude of parameter updates in deep learning. We provide a detailed theoretical analysis of the Grams optimizer, demonstrating its superior convergence properties compared to state-of-the-art cautious and momentum-based optimizers. Our experimental results on various datasets and models further validate the effectiveness of Grams in improving optimization efficiency and convergence speed. We believe that the Grams optimizer will serve as a valuable tool for optimizing deep learning models and contribute to the advancement of the field.

Code

#

The code of Grams has been open-sourced and is available on:

References

#