Paper Explained: SORSA - A Novel Approach to Parameter-Efficient Fine-Tuning

Table of Contents

See the original paper on arXiv.

Introduction
#

As large language models (LLMs) continue to grow in scale, fine-tuning them for specific tasks becomes increasingly expensive. Parameter-Efficient Fine-Tuning (PEFT) methods like LoRA have emerged as practical alternatives, but they face a critical challenge: catastrophic forgetting and overfitting in low-data regimes. When you fine-tune a model on mathematical problems, it might forget how to generate code or reason about common sense.

SORSA (Singular Values and Orthonormal Regularized Singular Vectors Adaptation) addresses this problem through a novel insight: maintaining well-conditioned weight matrices during training is crucial for preserving the model’s generalization capabilities.

Key Innovation
#

SORSA’s main contribution is an orthonormal regularizer that keeps singular vectors orthonormal during training. This seemingly simple addition has profound effects:

Better convergence: SORSA converges faster than LoRA and PiSSA
Improved generalization: Less catastrophic forgetting of pre-trained knowledge
Superior performance: On GSM-8K, Llama 2 7B with SORSA achieved 56.03% accuracy vs. LoRA’s 42.30% and even Full Fine-Tuning’s 49.05%

Background: Why Condition Numbers Matter
#

The condition number \(\kappa(W)\) of a weight matrix measures how sensitive the matrix is to perturbations:

\[ \kappa(W) = \frac{\sigma_{\max}(W)}{\sigma_{\min}(W)} \]

where \(\sigma_{\max}\) and \(\sigma_{\min}\) are the largest and smallest singular values.

Well-conditioned matrices (small \(\kappa\)) lead to:

Stable gradient flow
Better optimization landscapes
Preserved generalization from pre-training

Ill-conditioned matrices (large \(\kappa\)) cause:

Unstable training
Catastrophic forgetting
Poor generalization

Previous research has shown that neural networks with well-conditioned weights provide more robust performance. SORSA explicitly maintains this property during fine-tuning.

SORSA Architecture
#

SORSA begins with Singular Value Decomposition (SVD) of the pre-trained weight \(W_0\):

\[ W_0 = U\Sigma V^\top \]

The weight is then split into two components:

Principal weight \(W_p\) (trainable):
\[ W_p = U_p \cdot \text{diag}(S_p) \cdot V_p^\top \]
Residual weight \(W_r\) (frozen):
\[ W_r = U_r \cdot \text{diag}(S_r) \cdot V_r^\top \]

where the first \(r\) singular values go to \(W_p\) and the remaining go to \(W_r\).

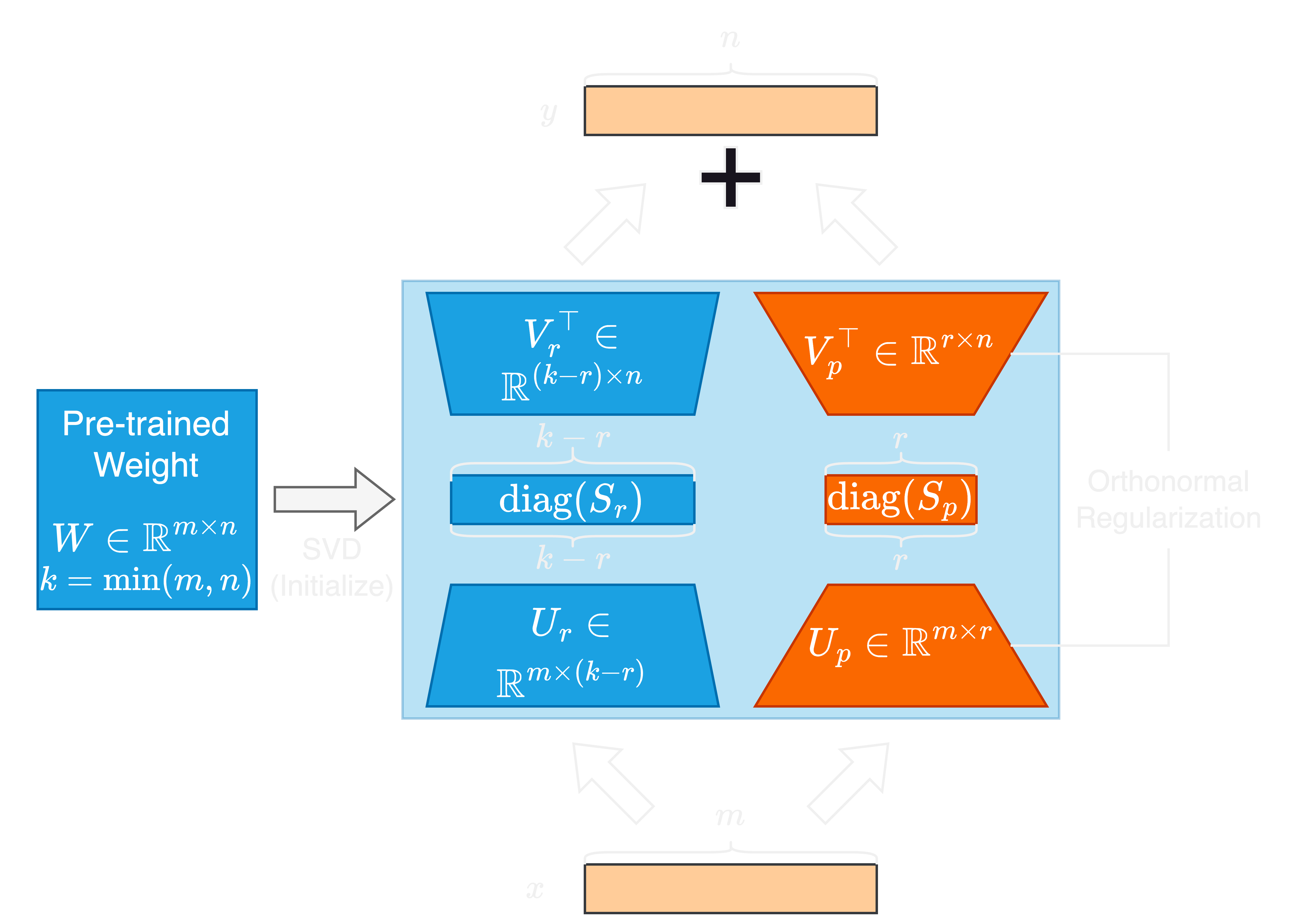
Key difference from PiSSA: While PiSSA merges the singular values into the matrices (\(A = U_p S_p^{1/2}\), \(B = S_p^{1/2} V_p^\top\)), SORSA keeps \(U_p\), \(S_p\), and \(V_p^\top\) separate. This separation enables the orthonormal regularizer to work effectively.

The Orthonormal Regularizer
#

SORSA’s secret sauce is the orthonormal regularizer:

\[ \mathcal{L}_{\text{reg}}(U_p, V_p) = \|U_p^\top U_p - I_m\|_F^2 + \|V_p^\top V_p - I_n\|_F^2 \]

This regularizer penalizes deviation from orthonormality, encouraging \(U_p\) and \(V_p\) to remain orthonormal throughout training.

Training Update Rule
#

The complete update at training step \(t\) is:

\[ W_{p,t+1} = W_{p,t} - \eta_t \nabla_{W_{p,t}} \mathcal{L}_{\text{train}} - \gamma_t \nabla_{W_{p,t}} \mathcal{L}_{\text{reg}} \]

where:

\(\eta_t\): learning rate for task loss
\(\gamma_t\): learning rate for regularizer
In practice, implemented as: \(\gamma_t = \frac{\gamma}{\eta_d} \eta_t\) where \(\eta_d\) is the maximum learning rate

Theoretical Analysis
#

Convergence Guarantees
#

Theorem (Linear Convergence): Under standard smoothness and strong convexity assumptions, SORSA with gradient descent converges linearly to the optimum:

\[ F(W_p^t) - F(W_p^*) \leq \left(1 - \frac{\mu_{\text{train}} - \gamma C_{\text{reg}}}{L_{\text{train}} + \gamma L_{\text{reg}}}\right)^t (F(W_p^0) - F(W_p^*) \]

This theoretical guarantee explains SORSA’s fast convergence in practice.

Condition Number Reduction
#

Theorem (Improved Conditioning): At every training iteration \(t\), the condition number of the regularized weight is strictly better than without regularization:

\[ \kappa(W_p^{\text{reg},t}) < \kappa(W_p^{\text{unreg},t}) \]

Proof sketch:

The regularizer drives \(U_p\) and \(V_p\) toward orthonormality, reducing \(\kappa(U_p)\) and \(\kappa(V_p)\)
Singular values are only slightly perturbed (by Weyl’s inequality)
Since \(\kappa(W) \leq \kappa(U)\kappa(\Sigma)\kappa(V)\), the overall condition number improves

This is the mathematical foundation for why SORSA preserves pre-trained knowledge better than other methods.

Experimental Analysis: What Changes During Fine-Tuning?
#

The paper introduces a novel analysis methodology to understand how fine-tuning affects the model’s internal structure:

Metrics
#

Singular Value Deviation:

\[ \Delta\Sigma_t = \frac{1}{k} \sum_{i=1}^k |\sigma_i^t - \sigma_i^0| \]

Singular Vector Deviation:

\[ \Delta D_t = 1 - \frac{1}{2k} \sum_{i=1}^k (|\langle u_i^t, u_i^0 \rangle| + |\langle v_i^t, v_i^0 \rangle|) \]

Key Findings
#

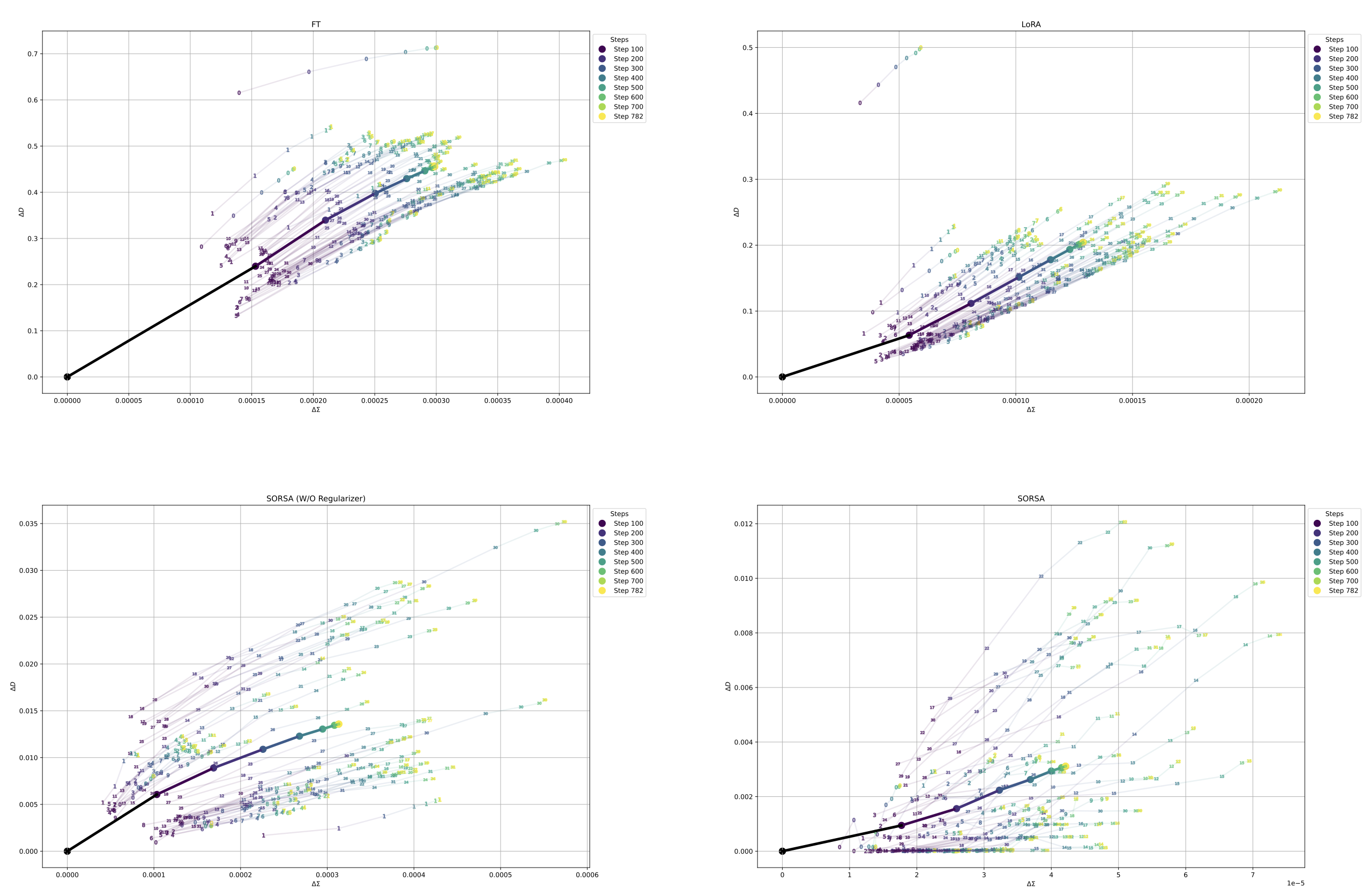
SORSA vs. LoRA/PiSSA:

LoRA and partial FT: Show large \(\Delta D\) (substantial disruption to singular vectors), indicating significant damage to pre-trained structure
PiSSA: Similar patterns to LoRA, with parallel updating across layers
SORSA: Dramatically smaller changes in both \(\Delta\Sigma\) and \(\Delta D\), with non-parallel, layer-specific updates

Interpretation: SORSA makes precise, targeted modifications while preserving the fundamental structure encoding the model’s general knowledge. The orthonormal regularizer acts as a constraint that prevents destructive changes to the weight matrices.

Experimental Results
#

Natural Language Generation Tasks
#

Training setup:

Models: Llama 2 7B, RWKV6 7B, Mistral 7B, Gemma 7B
Dataset: MetaMathQA (100K samples) → Evaluation on GSM-8K, MATH
Code: CodeFeedback (100K samples) → Evaluation on HumanEval

Performance Comparison
#

Model	Method	GSM-8K	MATH	HumanEval
Llama 2 7B	Full FT	49.05%	7.22%	21.34%
	LoRA	42.30%	5.50%	18.29%
	PiSSA	53.07%	7.44%	21.95%
	AdaLoRA	47.30%	6.48%	19.51%
	SORSA	56.03%	10.36%	24.39%
RWKV6 7B	LoRA	8.04%	7.38%	15.24%
	PiSSA	32.07%	9.42%	17.07%
	AdaLoRA	33.28%	8.08%	15.85%
	SORSA	45.87%	11.32%	22.56%
Mistral 7B	Full FT	67.02%	18.60%	45.12%
	LoRA	67.70%	19.68%	43.90%
	PiSSA	72.86%	21.54%	46.95%
	AdaLoRA	72.25%	21.06%	45.73%
	SORSA	73.09%	21.86%	47.56%

Key Observations
#

Llama 2 7B: SORSA shows the most dramatic improvements, outperforming even full fine-tuning by 7% on GSM-8K
RWKV6 7B: SORSA achieves 45.87% vs. LoRA’s catastrophic 8.04%, demonstrating robust learning
Gradient norms: SORSA maintains more consistent gradient norm reduction compared to LoRA and PiSSA, especially after ~300 training steps

Training Dynamics
#

The loss curves reveal interesting behavior:

Early training (0-300 steps): SORSA and PiSSA perform similarly
Late training (300+ steps): SORSA continues to decrease loss while LoRA/PiSSA plateau
Explanation: The orthonormal regularizer creates a better optimization landscape that sustains learning

Why SORSA Works: The Full Picture
#

SVD-based initialization: Starts from a meaningful decomposition of pre-trained weights
Separate components: Keeping \(U_p\), \(S_p\), \(V_p^\top\) separate (vs. merged in PiSSA) enables effective regularization
Orthonormal regularizer: Maintains well-conditioned matrices → stable optimization → preserved generalization
Targeted adaptation: Makes precise, layer-specific modifications rather than broad destructive changes

Practical Considerations
#

Advantages:

✅ No inference latency (adapters can be merged)
✅ ~80% VRAM reduction compared to full fine-tuning
✅ Faster convergence than LoRA/PiSSA
✅ Better generalization and less catastrophic forgetting
✅ Simple to implement

Hyperparameters:

Rank \(r\): 64-128 (similar to LoRA)
Regularizer weight \(\gamma\): 4e-4 to 5e-4
Learning rate: Slightly higher than LoRA (3e-5 vs. 2e-5) to counterbalance regularizer

Implementation
#

The code for SORSA is open-sourced:

Gunale0926/SORSA

SORSA: Singular Values and Orthonormal Regularized Singular Vectors Adaptation of Large Language Models

Python

Conclusion
#

SORSA represents a significant advancement in parameter-efficient fine-tuning by:

Identifying condition number as a critical factor in PEFT
Introducing an orthonormal regularizer to maintain well-conditioned weights
Providing theoretical guarantees on convergence and conditioning
Demonstrating substantial empirical improvements across multiple models and tasks

The key insight—that preserving the geometric structure of pre-trained weights through orthonormal regularization leads to better adaptation—opens new directions for future PEFT research.

Citation
#

@article{cao2024sorsa,
  title={SORSA: Singular Values and Orthonormal Regularized Singular Vectors Adaptation of Large Language Models},
  author={Cao, Yang and Song, Zhao},
  journal={arXiv preprint arXiv:2409.00055},
  year={2024}
}

Introduction #

Key Innovation #

Background: Why Condition Numbers Matter #

SORSA Architecture #

The Orthonormal Regularizer #

Training Update Rule #

Theoretical Analysis #

Convergence Guarantees #

Condition Number Reduction #

Experimental Analysis: What Changes During Fine-Tuning? #

Metrics #

Key Findings #

Experimental Results #

Natural Language Generation Tasks #

Performance Comparison #

Key Observations #

Training Dynamics #

Why SORSA Works: The Full Picture #

Practical Considerations #

Implementation #

Conclusion #

Citation #